문제 바로가기
https://www.acmicpc.net/problem/1018
1018번: 체스판 다시 칠하기
첫째 줄에 N과 M이 주어진다. N과 M은 8보다 크거나 같고, 50보다 작거나 같은 자연수이다. 둘째 줄부터 N개의 줄에는 보드의 각 행의 상태가 주어진다. B는 검은색이며, W는 흰색이다.
www.acmicpc.net
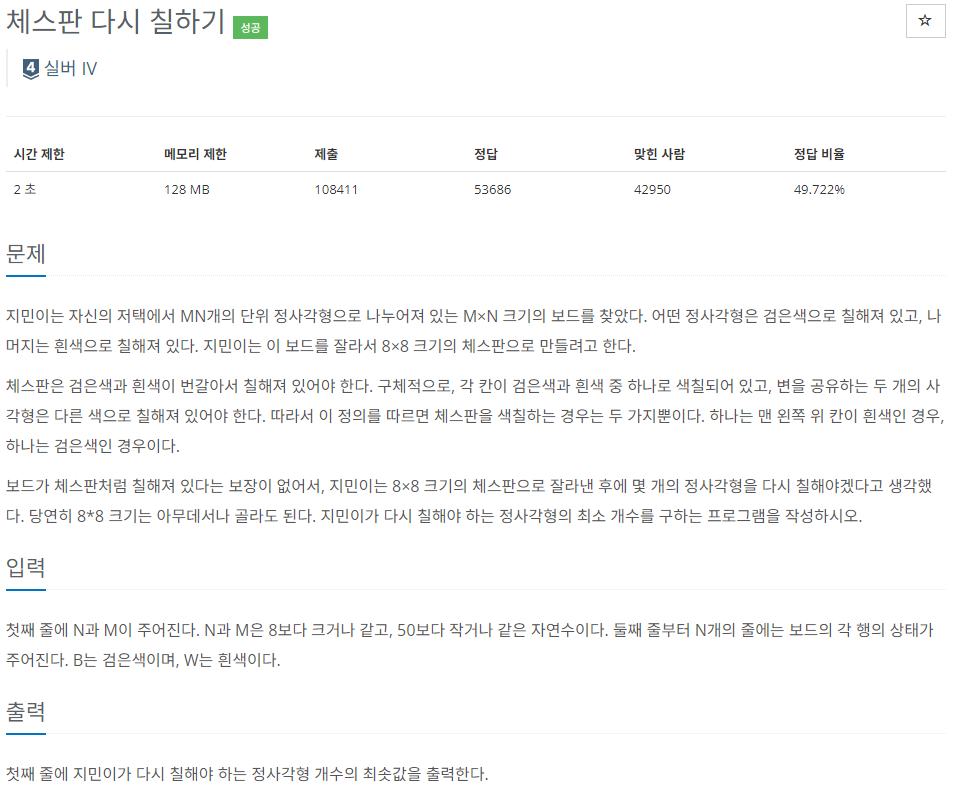

블로그 글의 가독성을 위해 예제 입력 2까지만 포함하여 작성하였다.
본 사이트에서는 더 많은 예제가 제공되어 있으니 입출력 예제가 필요한 경우엔 위 문제링크를 클릭하시기 바랍니다.
관련 알고리즘
- 브루트 포스
정답 및 해설
검은색과 흰색으로 칠해진 보드를 받아 8x8 사이즈의 체스판을 만들려고 한다.
주어진 보드의 일부분 혹은 전체를 사용하여 항상 검은색과 흰색이 번갈아가며 등장하는 체스판을 만들기 위해
다시 칠해야 하는 정사각형의 개수의 최솟값을 출력하는 문제이다.
예제 입력 1을 보면, 체스판으로 사용하기 위해서 4열 4행의 'B'를 'W'로 다시 칠하기만 하면 된다.
그 보다 적은 횟수로 체스판을 만들 수 있는 방법이 없기 때문에 정답이 1인 것이다.
보드 위의 모든 정사각형에 대하여 색칠을 해야 하는지 아닌지 체크하면서 그중 최솟값을 찾아야 하기 때문에
가능한 모든 경우를 체크해 보는 것이 가장 정확하다고 생각하여 브루트 포스로 문제를 해결하였다.
이 경우, 코드의 실행시간을 고려해야 하는데 보드의 최대 크기가 50x50으로 크지 않기 때문에 시간제한 내에 충분히 해결할 수 있다.
문제에서 주어진 것처럼 맨 왼쪽 위칸이 흰색인 경우 혹은 검은색인 경우 두 가지 체스판이 존재할 수 있다.
생각해 낸 방법은 완성된 체스판을 미리 준비해 두고 직접 가져다 대고 바꿔야 하는 칸의 개수를 세는 것이다.

위 그림과 같이 흰색과 검은색으로 시작하는 체스판을 미리 만들어 배열에 저장해 두고,
아래 그림처럼 입력받은 보드를 훑고 지나가며 색칠해야 하는 체스판의 개수를 세는 방법으로 풀이하였다.
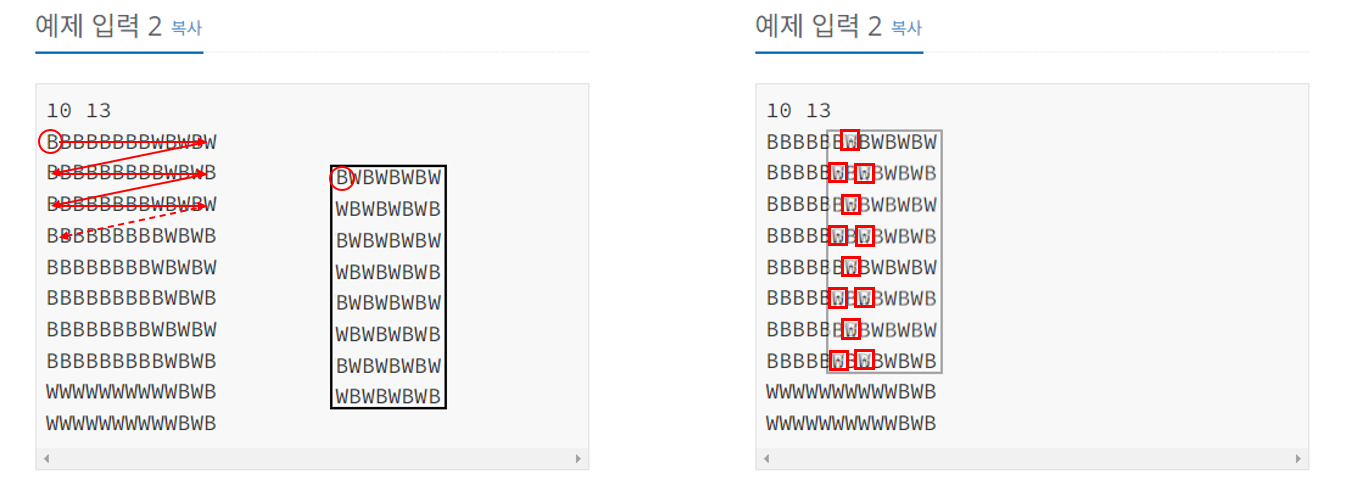
예제 입력 2를 예로 들면 좌측 그림과 같이 체스판을 들고 이동하면서 보드와 비교해서 바꿔야 하는 개수를 세는 것이다.
우측 그림과 같은 위치에서 최소 개수의 사각형을 다시 칠하여 체스판을 완성시킬 수 있다. (빨간색 사각형 12개)
C++
#include<bits/stdc++.h>
using namespace std;
int main(){
int N,M,ans,W_count=0,B_count=0;
char board[50][51];
char W[8][9]={"WBWBWBWB","BWBWBWBW","WBWBWBWB","BWBWBWBW",
"WBWBWBWB","BWBWBWBW","WBWBWBWB","BWBWBWBW"};
char B[8][9]={"BWBWBWBW","WBWBWBWB","BWBWBWBW","WBWBWBWB",
"BWBWBWBW","WBWBWBWB","BWBWBWBW","WBWBWBWB"};
cin>>N>>M;
ans=N*M;
for(int i=0; i<N; i++)
cin>>board[i];
for(int i=0; i<=N-8; i++)
for(int j=0; j<=M-8; j++){
W_count=0; B_count=0;
for(int k=0; k<8; k++)
for(int l=0; l<8; l++){
if(board[i+k][j+l]!=W[k][l]) W_count++;
if(board[i+k][j+l]!=B[k][l]) B_count++;
}
ans=min(ans,min(W_count,B_count));
}
cout<<ans;
}
| Line | 해설 |
| 4~5 | 풀이에 사용할 변수들을 선언합니다. int N,M : 각각 보드의 가로줄 수(Row), 세로줄 수(Colunm) int ans : 구할 정답 (바꿔야하는 사각형의 최소 개수) int W_count, B_count : 각각 흰색/검은색으로 시작할 때 바꿔야하는 사각형의 개수 char board[50][51] : 문제에서 입력받을 보드의 배열 |
| 6~9 | W[8][9]는 제일 왼쪽 위가 흰색으로 시작하는 완성된 체스판이고, B[8][9]는 제일 왼쪽 위가 검은색으로 시작하는 완성된 체스판입니다. 8x8 크기지만 배열이 [8][9]인 이유는 문자열 마지막에 문자열의 끝을 알리는 null('\0')를 포함하기 때문입니다. |
| 10~11 | 보드의 크기 N,M을 입력받고 ans를 최악의 경우 모든 사각형을 다시 칠해야한다는 가정하에 N*M으로 설정 |
| 12~13 | for 반복문을 이용해 board[i] 행에 보드의 배열을 입력받습니다. |
| 15~17 | for 문을 통해 반복에 들어갑니다. i와 j는 비교할 완성된 체스판의 가장 왼쪽 위 칸의 위치로 체스판 비교의 기준점으로 합니다. 반복이 시작함과 동시에 체스판 비교 후에 몇개의 사각형을 다시 칠해야할지 저장할 변수 W_count와 B_count를 0으로 초기화합니다. 이때 비교할 체스판이 8x8 크기이므로 i와 j의 범위를 잘 고려해야 OutOfBounds 오류를 막을 수 있습니다. |
| 18~22 | 위의 이중 for 문에서 i와 j로 기준점을 잡았다면 이제 k와 l로 체스판을 일일히 검사할 차례입니다. Line 20에서 board[i+k][j+l] (=기준점으로 부터 가로 k번째, 세로 l번째 사각형의 색깔)과 W[k][l](=왼쪽 위가 흰색인 체스판의 가로 k번째, 세로 l번째 사각형의 색깔)을 비교합니다. 만약 다르다면 해당 사각형을 다시 칠해야하므로 W_count를 1 증가시킵니다. Line 21에서 검정색 체스판을 이용해 동일한 방식으로 확인합니다. 이를 k와 l을 0~7 범위내에서 반복하여, 모든 사각형에 대하여 다시 색칠해야할 사각형의 개수를 W_count, B_count에 누적합니다. |
| 23 | min 함수를 사용하여 기존 최솟값, W_count, B_count 값 중 최솟값을 찾아 ans에 대입합니다. 이후 i와 j로 이루어진 반복문으로 돌아가 기준점을 한 칸씩 옮기면서 가능한 모든 경우에 대하여 체크합니다. |
| 25 | 모든 경우를 검사한 후에 그 중 가장 최솟값이 저장되어 있는 ans를 출력하여 정답을 구합니다. |
'Coding > BOJ' 카테고리의 다른 글
| [BOJ 백준] 1259 - 팰린드롬수 (C++) (0) | 2023.11.17 |
|---|---|
| [BOJ 백준] 1181 - 단어 정렬 (C++) (0) | 2023.11.16 |
| [BOJ 백준] 11720 - 숫자의 합 (C++ / Python) (0) | 2023.11.14 |
| [BOJ 백준] 10818 - 최소, 최대 (C++) (0) | 2023.11.14 |
| [BOJ 백준] 10809 - 알파벳 찾기 (C++) (0) | 2023.11.12 |

